|
 |

|

Р аздел "Штормовые нагоны Японского моря".
О бщая характеристика явления и условия
формирования штормовых нагонов в Японском море.
Штормовые нагоны представляют собой опасное гидрометеорологическое явление.
Их природа тесно связана с резким падением приземного атмосферного давления
и воздействием на морскую поверхность сильного ветра при прохождении над
прибрежной областью моря атмосферных образований типа циклонов или тайфунов.
Сочетание перечисленных факторов приводит к образованию значительных повышений
уровня моря у побережья. Кроме этого, быстродвижущиеся барические образования
в атмосфере могут генерировать длинную вынужденную волну в море (так называемое
"метеорологическое цунами"), которая при подходе к берегу также вызывает
повышение уровня моря. Во многом величина штормового нагона зависит от
морфометрических особенностей отдельных участков побережья.
В совокупности с приливо-отливными колебаниями уровня и штормовым волнением
штормовые нагоны создают угрозу для прибрежных районов и могут служить помехой
при выполнении различных инженерных и хозяйственных работ, снижая их эффективность.
Обусловленные штормами подъемы уровня могут достигать и превышать критические отметки,
при которых возникают катастрофические ситуации, приводящие к наводнениям, затоплению
отдельных участков суши, разрушению портовых сооружений и хозяйственных объектов,
расположенных вблизи береговой черты.
Наглядным примером сказанному могут служить случаи штормовых нагонов, которые нанесли
заметный ущерб в южной части о. Сахалин. Так, в течение 1990 г. дважды происходили серьезные
повреждения специально построенного бетонированного откосного берегоукрепительного
сооружения на станции Холмск - сортировочная, спроектированного для перегрузки вагонов,
прибывающих на остров паромной переправой из порта Ванино. Первые разрушения были вызваны
штормовым нагоном 7 апреля 1990 г., когда станция находилась еще в стадии завершения
строительства. По данным гидрометеослужбы, шторм был рядовой - высота волнения не превышала
2,2 м. Но оно наблюдалось на фоне достаточно сильного нагона ( до 0.7 м, что близко к
максимальному для данного места. В ноябре 1990 г. в рассматриваемом районе наблюдался
самый сильный нагон за весь период наблюдений (около 1 м), соответствовавший периоду
повторяемости 1 раз в сто лет. Нагон нанес чрезвычайный ущерб Холмской дистанции железной
дороги, в частности, стоимость разрушенного бетонированного откосного укрепления составила
1.6 млн. рублей в старом исчислении. С учетом косвенного ущерба, связанного с задержкой
вагонов и нарушением режима работы паромной переправы, сумма ущерба оказалась еще более значительной
Согласно , синоптические условия формирования штормовых нагонов на побережье
Японского моря сводятся к прохождению над акваторией моря циклонов 4-х типов. В
исследованиях, посвященных данному вопросу [Фирсов,1988,1989; Фирсов, Савельев,2002],
отмечается, что преобладающее число штормовых нагонов ( до 80 %) формируется под
действием выходящих на Японское море интенсивных южных циклонов и тайфунов. Как правило,
значительные нагоны происходят при перемещении тайфунов над центральной частью моря в
северном или северо-восточном направлении. Сильные ветры при этом имеют направление от
южного до северо-восточного.
Давление в центре таких барических образований составляет 970-980 гПа,
максимальные градиенты атмосферного давления в передней части циклонов
составляют 20-25 гПа/300 км, Средняя скорость движения циклонов равна 40-45 км/ч,
уменьшаясь по мере продвижения на север.
Вследствие небольших приливных колебаний уровня в Японском
море штормовые нагоны здесь играют определяющую роль в развитии
экстремальных подъемов уровня. Естественно, что интенсивность
и характер экстремальных подъемов уровня определяется не только
синоптическими условиями. Генерация штормовых нагонов, их интенсивность
и продолжительность во многом зависят от ориентации и конфигурации
береговой черты, рельефа дна и ширины шельфа в отдельных районах
побережья моря. Кроме этого важным фактором формирования нагонов является
направление ветра и продолжительность действия эффективного (т.е. наиболее
благоприятного по направлению для формирования нагона) ветра. Так,
например, исследования, выполненные для побережья Приморского края [Савельев,
Фирсов, 2000], показывают, что в заливе Петра Великого нагоны формируются под
действием ветров четырех направлений: южного, юго-восточного, восточного
и северо- восточного. Максимальные нагоны наблюдаются при юго-восточных и
восточных ветрах. В центральной части Приморья (Рудная Пристань) наибольшая
повторяемость и интенсивность нагонов отмечается при северо-восточных и восточных ветрах.
В северной части Татарского пролива в возникновении нагонов основную
роль играют ветры южных румбов. Согласно опубликованным источникам
[Фирсов,1988; Любицкий и др.,1994], нагоны здесь формируются при
прохождении глубоких циклонов по двум характерным траекториям. Большинство
нагонов (70% случаев) возникает при перемещении южных циклонов над Японским
морем, Татарским проливом в сторону Сахалинского залива или в район,
расположенный северо-восточнее о. Сахалин. Реже (18%) нагоны формируются
континентальными циклонами, выходящими с Амурской области или северного Китая
на акваторию Охотского моря, а также (12%) при совместном влиянии
континентального и южного циклонов.
С ведения об исходной информации уровенных наблюдений
в Японском море, на основе которых выполнен анализ
штормовых нагонов, методика их выделения.
Характеристика исходной информации.
Хтарактеристика рядов наблюдений за уровнем
на отечественном побережье Японского моря,
которые послужили основным исходным материалом
для выделения и анализа штормовых нагонов,
представлена в Местоположение пунктов
наблюдений за уровнем моря иллюстрирует
- Расположение пунктов наблюдений за уровнем на
отечественном побережье Японского моря.
Как следует из таблицы 1, исходная информация по уровню Японского моря
неоднородна, во многих пунктах производились как ежечасные, так и срочные
наблюдения. Срочные наблюдения не использовались при анализе нагонов,
поскольку все методики выделения нагонов из суммарных колебаний уровня предполагают
использование только ежечасных значений уровня. Кроме этого, первые годы наблюдений
в отдельных пунктах (например, Находка, Рудная Пристань, Сов.Гавань, Холмск) также не
использовались для анализа нагонов из-за больших перерывов в наблюдениях, либо
отсутствия материалов. Последние годы отдельных пунктов по объективным причинам
были недоступны для использования.
Поэтому анализ штормовых нагонов выполнялся
на основе всего имеющегося доступного материала.
Выделение штормовых нагонов.
В связи с тем, что анализ штормовых нагонов выполнялся
различными авторами, использовалось 2 различных подхода
к их выделению из исходных суммарных уровней. В большинства
пунктов нагоны определялись путем вычитания из суммарного уровня
моря предвычисленного прилива [Шевченко, Любицкий, Като,1994; Шевченко, 1997;
Фирсов,1988,1989; Фирсов, Савельев,2000; Като, Миськов, Шевченко,2001].
Гармонические постоянные (полуамплитуды и фазы) приливов, по которым
предвычислялся прилив, рассчитывались по методу наименьших квадратов
(МНК). Наилучшее исключение прилива (суточного и полусуточного) было
достигнуто при числе приливных гармоник, равных 21. Метод наименьших
квадратов, благодаря своей простоте, гибкости и сравнительно высокой
точности, получил широкое распространение при анализе приливов [ Zetler B.D.,
Lennon G.W., 1967; Godin G., 1970; Куликов Е.А., Рабинович А.Б., Харви Р.Р.,
1977; Макаева О.С., 1977]. В отличие от классических методов Дарвина и Дудсона,
которые для расчета гармонических постоянных требуют использования не менее
месячной серии ежечасных значений уровня моря, при использовании МНК для
получения такого же количества гармонических постоянных достаточно полумесячной серии.
Метод заключается в следующем. В соответствии с
теорией гармонического анализа, исходная формула для расчета приливов имеет вид:
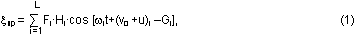
где F- редукционный множитель i-той волны;
H - средняя полуамплитуда приливного уровня;
G - угол положения (фаза) волны;
 - угловая скорость волны;
- угловая скорость волны;
t - время;
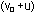 - начальный астрономический аргумент волны;
- начальный астрономический аргумент волны;
L - число гармонических постоянных.
Для использования МНК формулу (1) удобно
представить в виде:
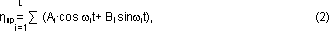
где

Метод наименьших квадратов заключается в отыскании
таких значений коэффициентов Ai и Bi , которые
минимизировали бы выражение:

где 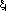 - наблюденный уровень в j- тые моменты времени,
- наблюденный уровень в j- тые моменты времени, 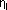 - определяется по формуле (2), N- число отсчетов.
- определяется по формуле (2), N- число отсчетов.
Таким образом, задача сводится к решению системы линейных уравнений порядка 2L+1, где L
- число рассчитываемых гармоник:

Вычислив таким образом гармонические постоянные
L - числа волн, предвычисление прилива осуществляется согласно формуле (1).
Другой метод, использованный для нескольких пунктов северной
части Татарского пролива (Де - Касти, Александровск-Сахалинский), основан на выделении штормовых
нагонов из суммарных наблюденных уровней 25-ти часовым скользящим осреднением. Поскольку при такой
фильтрации прилива частично срезается и непериодическая составляющая, максимумы нагонов
восстанавливались методом Г.А. Баскакова [ Баскаков, 1973]. Баскаков указывает, что в
этом случае занижение максимума нагона равняется половине приращения уровня в сутки. Поэтому,
считая первым приближением максимальный непериодический уровень h'n, полученный при фильтрации,
исправленный уровень h''n вычисляется из следующего соотношения:

где 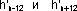 - непериодические колебания уровня для моментов n-12 и n+12 часов до максимума.
Р ежимные характеристики штормовых нагонов в
Японском море, их пространственно - временная изменчивость.
- непериодические колебания уровня для моментов n-12 и n+12 часов до максимума.
Р ежимные характеристики штормовых нагонов в
Японском море, их пространственно - временная изменчивость.
За период нагона принимался интервал времени, на протяжении которого
непериодические ( бесприливные ) колебания уровня были выше среднего уровня моря.
За нагон принимались лишь такие непериодические повышения уровня,
высота которых над средним была равна или превышала 20 см над средним уровнем моря, поскольку колебания
уровня ниже этой отметки незначимы и никакой существенной опасности не представляют.
Для удобства анализа штормовые нагоны были условно разделены на группы,
отличающиеся по своей интенсивности:
- слабые ( < + 40 см относительно среднего уровня);
- умеренные ( +40-69 см относительно среднего уровня);
- сильные ( +70-99 см относительно среднего уровня моря);
- экстремальные (> +100 см относительно среднего уровня).
Результаты статистической обработки рядов нагонов представлены на рисунке
3 и в таблицах 2-5. Общее количество нагонов, использованных для анализа, указано в таблице 5.
Анализ кривых внутригодового распределения нагонов в Японском море
() показывает, что
наибольшее число их в южной части побережья Приморья наблюдается в августе-сентябре.
Приморья наблюдается в августе-сентябре. В южной части Татарского пролива
(Золотой, Советская Гавань, Углегорск, Холмск) максимум повторяемости нагонов смещен на октябрь-ноябрь.
Отличительной особенностью северной части Татарского пролива является наличие ярко выраженного максимума
повторяемости и интенсивности нагонов - в апреле и в осенне-зимний период (октябрь-декабрь).
Из таблиц 2-4 следует, что в южной части побережья Приморья (Посьет-Преображение),
а также в северной части Татарского пролива (Сов.Гавань, Александровск) наблюдаются только слабые и умеренные
нагоны, максимальная высота которых составляет около 0.6 м над средним уровнем моря, средняя высота нагона не
превышает 30 см. Наибольшие высоты нагонов отмечаются в центральной части побережья Приморья на участке Рудная
Пристань - Золотой). Повторяемость сильных нагонов (70-99 см) здесь достигают 14-18%. Максимальный наблюденный
нагон в Рудной Пристани составлял 123 см. Здесь же отмечаются и случаи экстремальных ( более 1 м) нагонов,
хотя повторяемость их мала и не превышает 1%. Средняя высота нагона варьирует в пределах 45-55 см. Сильные
нагоны наблюдаются также в южной части побережья о. Сахалин (Углегорск, Холмск) с повторяемостью около 2 -3 %.
Максимальная величина нагона в этом районе доходила до 97 см (Холмск).
Характерные изменения уровня при нагонах иллюстрирует таблица 5.
. Повторяемость
(P) высот нагонов над средним уровнем в пунктах побережья Японского моря.
.
Повторяемость (P) высот нагонов над средним уровнем в пунктах побережья Японского моря.
.
Средние и максимальные высоты штормовых нагонов в сантиметрах относительно среднего уровня моря
в отдельных пунктах побережья Японского моря.
(в числителе - максимальные высоты, в знаменателе - средние высоты нагонов).
.
Характеристики максимальных и средних нагонов в отдельных пунктах побережья Японского моря
(в числителе - характеристики максимальных нагонов, в знаменателе - средних).
Отличительной чертой нагонов побережья Японского моря является их асимметрия:
фаза подъема уровня (Т2)круче, чем фаза спада. Исключением является Татарский пролив, где фаза
роста и падения уровня практически одинаковы. Средняя продолжительность нагонов варьирует от 2.5 до 4.5 суток.
Конечно, ограниченная продолжительность рядов уровенных
наблюдений не позволяет получить достаточно надежные характеристики редко встречающихся
значительных (повторяемостью 1 раз в 50 лет, 1 раз в 100 лет и т.д.) нагонов. Для оценки
высот штормовых нагонов редкой повторяемости в отдельных пунктах побережья о. Сахалин в работе
Э.Като и др. [ Като, Миськов, Шевченко, 2001] использовался метод двойного экспоненциального закона
[ Герман,1971; Герман, Левиков,1988; Руководство,1973]. Аналогичные оценки для пунктов центрального
побережья Приморья, где наблюдаются экстремальные нагоны, приводятся в научно - справочном монографическом
пособии " Гидрометеорология и гидрохимия морей " [Фирсов, 1992; Фирсов, Савельев,2002]. Основа метода
состоит в аппроксимации эмпирической кривой распределения, построенной по наблюдениям, теоретической
функцией, при помощи которой можно экстраполировать эмпирическую кривую в область редких повторяемостей.
Теоретическая функция имеет следующий вид:

где P - функция распределения, y - вспомогательная или приведенная переменная экстремальных значений.
Результаты оценки нагонов редкой повторяемости сведены в
.
Согласно приведенным оценкам, экстремально возможные нагоны могут достигать 1.5 м
на побережье Приморья и 0.9 м в южной части о. Сахалин.
О писание моделей, связанных с анализом
и прогнозом штормовых нагонов в Японском море.
Численное моделирование штормовых нагонов.
Постановка задачи.
Для расчета и прогноза штормовых нагонов
в отдельных пунктах побережья Японского моря использованы уравнения мелкой воды [ Вольцингер
Н.А., Пясковский Р.В.,1968,1977]. Двумерная система проинтегрированных по глубине уравнений
движения и неразрывности имеет следующий вид:

Компоненты напряжения ветра на поверхности
моря и придонного трения рассчитываются с помощью квадратичных соотношений:
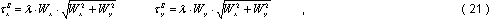
где  - коэффициент поверхностного трения;
Wx , Wy - проекции скорости ветра на оси координат; - коэффициент поверхностного трения;
Wx , Wy - проекции скорости ветра на оси координат;

где r - коэффициент придонного трения.
Решение этой системы уравнений требует постановки начальных и граничных условий.
На твердой границе, расположенной на берегу, нормальные компоненты скорости равны нулю. На жидкой границе
возвышение уровня принимается равным нулю, если не учитывается эффект атмосферного давления.
В том случае, когда необходимо учесть влияние на уровень вариаций атмосферного
давления, условие на жидкой границе принимает вид:

где P - среднее атмосферное давление над исследуемым районом;
P - атмосферное давление на жидкой границе.
Начальные условия принимались нулевыми: 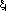 = 0, U = 0, V = 0 при t = 0. = 0, U = 0, V = 0 при t = 0.
Для решения уравнений применялась явно-неявная схема с конечно-разностной сеткой
типа "С" [Tong Yongmin, Sun Wenxin, Feng Shizuo,1990; Sun Wenxin, 1992]. При этом каждый шаг по времени
разбивается на 2 полушага. На первом полушаге решается уравнение по явной схеме определяются значения
компоненты скорости V в момент времени n + 1/2. Затем, используя полученные значения V, по неявной схеме
решается уравнение для определения U -компоненты течения. В конечном итоге из уравнения неразрывности по
известным значениям U и V рассчитываются возвышения уровня в конкретной точке сеточной области.
При использовании конечно-разностной сетки типа "С" значения компонент скорости
течения вычисляются непосредственно в узлах сетки, а значения возвышения уровня - в центре квадратов
сеточной области. Однако для решения уравнения неразрывности необходимо знать значения U и V в центре
квадратов сеточной области, для чего выполняется их осреднение по четырем точкам в каждом квадрате.
На втором полушаге этот процесс повторяется.
Все пространственные производные рассчитываются со вторым порядком точности.
Численная схема не требуют жесткой зависимости между временным и пространственным шагами и позволяет их
выбирать оптимальными. Принятая постановка задачи позволяет рассчитывать пространственно-временные изменения
уровня моря во время реальных штормовых нагонов по фактическим значениям параметров ветра и приземного
атмосферного давления над морем.
Область расчета и исходные данные.
Расчет штормовых нагонов выполнялся для акватории залива
Петра Великого [Saveliev, Firsov, 1996; Савельев, Фирсов,2000; Фирсов, Савельев, 2002].
Согласно рисунку 4, область расчета простирается от м. Поворотный до устьевого района реки
Туманган и охватывает более мористую область, ограниченную меридианами 130О12' и 134O 00' в.д.
и параллелями 42O 00'и 43O15' с.ш. Пространственный шаг сетки выбран 3' (5.6 км) по меридиану.
. Расчетная сетка для
расчета штормовых нагонов на акватории залива Петра Великого.
Верификация модели и результаты численного моделирования.
Верификация модели проводилась по двум сериям экстремальных нагонов, наблюденных в
пунктах Посьет, Владивосток, Находка во время штормовых ситуаций 25-28 октября 1980 г.
и 27-30 августа 1982 г.
В качестве исходной метеорологической информации использовались
расчетные значения атмосферного давления и характеристик ветра. Для учета пространственно-временной
изменчивости полей атмосферного давления его значения снимались по фактическим приземным
синоптическим картам в 15 точках (см. рисунок 4), равномерно распределенных в пределах исследуемой
области, с дискретностью 6 ч. Далее выполнялась процедура интерполяции значений давления в узлы сеточной
области. Характеристики ветра рассчитывались по градиентному ветру в соответствии с методикой
А.И. Соркиной [Соркина,1958] и принимались однородными для всей области расчета, что не противоречит
реальным условиям при штормовых ситуациях.
Результаты численных экспериментов, приведенные на
, показывают, что
высоты рассчитанных и наблюденных штормовых нагонов хорошо согласуются. Имеются лишь незначительные
различия во временном ходе кривых, особенно заметные на фазе падения уровня и в моменты наступления максимумов.
Средняя ошибка расчета максимумов нагонов не превысила 9 см, что позволяет считать
результаты модельных расчетов в целом удовлетворительными.
Результаты моделирования представлены в виде номограмм, характеризующих
чисто ветровые подъемы уровня в зависимости от различных направлений и скоростей ветра в 4-х пунктах
залива Петра Великого ().
Расположение точек представлено на
Анализ результатов показывает, что штормовые нагоны в данном районе формируются под
действием ветров четырех направлений: южного, юго-восточного, восточного и северо- восточного.
Максимальные нагоны возникают при юго-восточных и восточных ветрах и могут достигать значений
от 70-80 см в районе реки Туманган до 100-115 см в остальных пунктах при скорости ветра 40 м/с.
При штормовых южных ветрах (30-40 м/с) в пунктах Владивосток и Находка могут формироваться нагоны
до 50-60 см над средним уровнем моря, в то время, как в районе Посьета и реки Туманган при тех же
метеорологических условиях величины нагонов незначительны.
Представленные на рисунке номограммы могут быть легко использованы в
практике прогнозирования штормовых нагонов в заливе Петра Великого в том случае, если имеется
прогностическая информация о параметрах ветра.При этом дополнительно для более точного предсказания
высоты нагона необходимо учитывать влияние перепадов атмосферного давления на уровень моря. Указанное
влияние учитывается при помощи поправки к высоте ветрового нагона, рассчитанной согласно соотношению
"обратного" барометра (отклонение давления от среднего на 1 гПа соответствует отклонению уровня на 1 см
с обратным знаком).
Метод спектральной регрессии.
При статистическом анализе связи между непериодическими
колебаниями уровня и вынуждающими силами обнаруживается два основных подхода. Наиболее
часто используется обычная линейная регрессия, которая позволяет определить для каждой
вынуждающей силы свой единый коэффициент влияния, который может рассматриваться как некоторый
средний для всего диапазона частот. Достаточно часто коэффициенты линейной корреляции, а соответственно,
и коэффициенты влияния (регрессии), определенные таким путем, оказываются низкими, особенно для вынуждающих
сил, имеющих существенные резкие энергетические всплески в отдельные короткие периоды и относительно небольшие
величины на протяжении всего остального времени ( такой вынуждающей силой, например, может служить ветер).
Однако из этого не следует вывод о слабой связи между процессами. Достаточно тесная
связь может иметь место, но в каком-либо определенном интервале частот. Это приводит к необходимости применения
спектральных методов для исследования и расчета непериодических колебаний уровня моря [Hamon, Hannan, 1963; Герман,
1975; Савельев, Герман, 1986]. Метод более перспективен по сравнению с обычным методом линейной регрессии,
поскольку позволяет учесть сложную внутреннюю структуру процесса и определить связь между исследуемыми параметрами
в искомом (энергонесущем для взаимной спектральной функции) диапазоне частот. По методу спектральной регрессии
связь определяется посредством расчета так называемых "угловых" коэффициенты регрессии как средневзвешенных
оценок в исследуемом диапазоне частот, на котором эта связь максимальна.
На основе указанного метода П.Б. Фирсовым [Фирсов, 1984; Фирсов, Савельев, 2002]
был разработан метод расчета и прогноза штормовых нагонов в пунктах Находка и Рудная Пристань. В качестве
вынуждающих сил использовались временные ряды коэффициентов разложения барического поля по естественным
ортогональным функциям (е.о.ф.) B0, B1 ,B2 ,B3 ,B4 , которые физически отражают некоторое среднее состояние
барического поля, его меридиональную, зональную изменчивость, процессы более мелких масштабов (вихри и.д.),
соответственно. Коэффициенты уравнений определяются по спектральным характеристикам процессов и представляют
собой действительную часть передаточной функции на частотах с максимальными значениями функции множественной
когерентности. Как оказалось, наилучшую связь между непериодическими колебаниями уровня показали первые два
коэффициента разложения поля давления, которые и использовались для построения уравнений спектральной регрессии
().
К аталог максимальных
нагонов и исторический календарь сведений об ущербе,
нанесенном нагонами на побережье Японского моря.
В
приведен каталог максимальных нагонов для отдельных
пунктов отечественного побережья Японского моря. Сведения о максимальных годовых нагонах для пунктов
побережья о. Сахалин (Углегорск, Холмск) взяты из работ [Шевченко, Любицкий, Като, 1994; Шевченко, 1997].
Надо заметить, что сама по себе высота подъема уровня во время нагона мало что
говорит о степени опасности этого стихийного явления в том или ином пункте. Чтобы составить представление о
связанном с ним риске, важно иметь сведения о последствиях сильных нагонов. Как указывалось ранее, экстремальные
нагоны в Японском море отмечаются в центральной части побережья Приморья на участке Рудная Пристань - Золотой.
Однако непосредственно никакой серьезной опасности нагонные повышения уровня на материковом побережье не
вызывают, вследствие чего сведения об ущербе от штормовых нагонов здесь отсутствуют. Тем не менее, успешность
гидротехнического строительства и проведение рейдовых грузовых операций в портпунктах, а также развитие прибрежного
рыболовства и геологических изысканий во многом зависит здесь от информации о штормовых нагонах.
Существенный ущерб от штормовых нагонов отмечается только на юго-западном побережье
о. Сахалин ( участок Углегорск - Невельск). По-видимому, это определяется орографическими особенностями побережья,
мелководностью района, а также траекториями смещения циклонов, формирующих нагоны, значительная часть которых
пролегает именно вблизи указанного района. Специального учета сведений об ущербе нигде не ведется. Поэтому в
таблице 9 приводится сведения об ущербе от наиболее сильных нагонов на юго-западном побережье о. Сахалин,
включающие в себя фрагментарные данные за последнее десятилетие, собранные из опубликованных источников
[Шевченко, Любицкий, Като,1994; Шевченко, 1997; Като, Миськов, Шевченко, 2001]. Как правило, больше всего от
штормовых нагонов страдает транспортная система южной части Сахалина - морское, железнодорожное и автомобильное
сообщение. Большинство морских портов прекращают работу при штормовых ситуациях, случаются заливания
отдельных причалов, портовых складских и иных сооружений, смываются в море или портятся находящиеся в
портах грузы, что приводит к большому ущербу.
Сведения об ущербе от сильнейших штормовых нагонов на
юго-восточном побережье о.Сахалин в последнее десятилетие.
С писок использованных источников:
1. Баскаков Г.А. Выделение непериодической составляющей из суммарных
колебаний уровня // Проблемы Арктики и Антарктики. - 1973. - Вып.41. - С.17-23.
2. Вольцингер Н.Е., Пясковский Р.В. Основные океанологические задачи теории
мелкой воды. - Л.: Гидрометеоиздат, 1968. - 300 с.
3. Вольцингер Н.Е., Пясковский Р.В. Теория мелкой воды. - Л.: Гидрометеоиздат,
1977. - 207 с.
4. Герман В.Х. Исследование и расчет вероятностных характеристик экстремальных
уровней моря // Тр. ГОИН. - 1971. - Вып.107. - 105 с.
5. Герман В.Х. Связь колебаний уровня мелкого моря с вынуждающими силами в
синоптическом диапазоне частот // Труды ГОИН. - 1975.- Вып. 126. - С. 8-19.
6. Герман В.Х., Левиков С.П. Вероятностный анализ и моделирование колебаний уровня
моря. - Л.: Гидрометиздат, 1988. - 231 с.
7. Като Э., Миськов О.А., Шевченко Г.В. Штормовые нагоны на побережье острова
Сахалин в конце XX века // В сб.: Динамические процессы на шельфе Сахалина и Курильских
островов. - Южно-Сахалинск: ИМГи Г ДВО РАН,2001. - С.160-176.
8. Куликов Е.А., Рабинович А.Б., Харви Р.Р. Глубоководные исследования приливов в
северо-западной части Тихого океана // Гидрофизические исследования океана. - Труды СахкНИИ. - 1977. - Вып.54. - С.
59-75.
9. Любицкий Ю.В., Маринченко И.Ф., Шевцов А.Е. Сгонно-нагонные колебания уровня
моря в северной части Татарского пролива // Известия РГО. - 1994.- Т.126, Вып.1. - С. 48-53.
10. Макаева О.С. Гармонический анализ приливов методом наименьших квадратов //
Труды ГОИН. - 1977. - Вып. 138. - С. 38-43.
11. Руководство по расчету элементов гидрологического режима в прибрежной зоне морей
и в устьях рек при инженерных изысканиях. -Л.: Гидрометиздат, 1973. - 535 c.
12. Савельев А.В., Герман В.Х. Расчет штормовых нагонов в Охотском море методом
спектральной регрессии // Океанология. - 1986. - Т. XXVI. - С.409-415.
13. Савельев А.В., Фирсов П.Б. Применение численной модели для расчета и прогноза
штормовых нагонов на побережье Приморья // Труды ДВНИГМИ. - 2000. - Вып.140. - С.3 - 11.
14. Соркина А.И. Построение карт ветровых полей для морей и океанов // Труды
ГОИН. - 1958. - Вып.44. - 74 с.
15. Фирсов П.Б. Статистическая структура непериодических колебаний уровня на
побережье Японского моря // Труды ГМЦ СССР.- 1984. - Вып.263. - С.41-52.
16. Фирсов П.Б. О механизме формирования штормовых нагонов в северной части
Японского моря // Труды ДВНИГМИ. - 1988. - Вып.132. -С.3-21.
17. Фирсов П.Б. К вопросу об изменчивости непериодических колебаний уровня моря
на побережье Японского моря // Труды ДВНИГМИ. -1989. - Вып.39. - С.86-97.
18. Фирсов П.Б. Расчет экстремальных подъемов уровня в северной части Японского
моря // Труды ДВНИГМИ. - 1992. - Вып.145. - С.21-38.
19. Фирсов П.Б., Савельев А.В. Непериодические колебания уровня Японского моря
// В кн.: Гидрометеорология и гидрохимия морей. Том XI. Японское море. Вып. 1. Гидрометеорологические условия.
- С-Пб.: Гидрометеоиздат, 2002. ( в печати).
20. Шевченко Г.В. Статистические характеристики штормовых нагонов в южной части
о. Сахалин // Изв. РГО. - 1997. - Т.129, Вып.3. - С.94 - 106.
21. Шевченко Г.В., Любицкий Ю.В., Като Л.Н. Проявление штормовых нагонов в
южной части острова Сахалин. - Южно-Сахалинск: ИМГ и Г ДВО РАН, 1994. - 46 с.
22. Godin G. The resolution of tidal constituents // Int. Hydr. Rev. - 1970.
- Vol.47, №2. - P.133-144.
23. Hamon B.V., Hannan E.J. Estimating relations between time series // Journ.
Geophys. Res. - 1963. - Vol. 68, № 21. - P.6033-6042.
24. Sun Wenxin Three-dimensional shallow water hydrodynamical numerical
method - velocity splitting method // In: The Numerical Computation of Physical Oceanography. - Henan Sciebce
& Technology Press, 1992. - P.3 - 12.
25. Tong Yangming, Sun Wenxin, Feng Shizuo Method of separating of the
three-dimensional shallow water hydrodynamical model // In: Storm Surge: Observations and Modelling. - China
Ocean Press, 1990. - P. 10-20.
26. Zetler B.D., Lennon G.W. Some comparative tests of tidal analytical
processes. - Int. Hydr. Rev. - 1967. - Vol.44, №1.- P.139-147.
|
 |